Robert Markweger
Lineare und Quadratische Gleichungen
Auch eine Funktion wird im Prinzip ganz einfach nach Links und nach Rechts aufgetragen.
Erst durch die Vereinbarung das Vorzeichen der Linken Seite, also der
als Negativ definierten Seite, gleichzeitig als ein Negationszeichen zu
verwenden entsteht ein Unterschied.
Lineare Gleichungen
Hier ist zunächst eine ganz
einfache lineare Funktionsgleichung.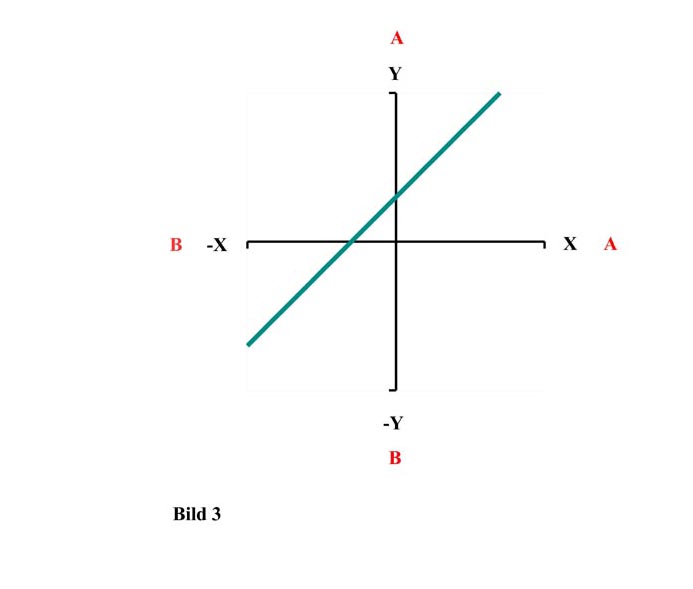
y = x + d
Und die Lösung für y = 0
x + d = 0
x = -d
Man kann es natürlich genau so gut aus der
entgegengesetzten B-Richtung betrachten:
y = x - d
x - d = 0
x = d
Beides führt zum gleichen Ergebnis nur eben aus der jeweils gegenteiligen Richtung betrachtet.
Dass allerdings in A-Richtung
betrachtet (-d) Sinn macht setzt bereits
voraus dass eine Funktion auch in die Gegenrichtung definiert ist, was
nicht zwangsläufig sein muss. Denn genau genommen ist immer eine
Funktion in die eine Richtung definiert (A) und eine Funktion in die
Gegenrichtung (B), es sind eigentlich zwei Funktionen.
Wenn eine Lösung aus der
A-Richtung betrachtet Positiv ist, so ist
sie eben aus der B-Richtung betrachtet Negativ und umgekehrt wenn eine
Lösung aus der A-Richtung betrachtet Negativ ist, so ist sie eben
aus B-Richtung betrachtet Positiv.
Man kann es auch genau so gut als eine Funktion in A-Richtung und eine Funktion in B Richtung über X aufgetragen betrachten:
Die A-Richtung ist wieder:
y = x + d
x + d = 0
x = -d
Und die B-Richtung ist dann:
y = -x + d
-x + d = 0
x - d = 0
x = d
Es sind letztendlich immer zwei Funktionen eine in die eine Richtung und eine in die Gegenrichtung aufgetragen, nichts sonst.
Natürlich ist nichts falsch daran wenn man diese beiden Funktionen
zusammenfügt und in der üblichen Form als eine Funktion betrachtet, sofern man
sich dessen bewusst ist dass eigentlich zwei Funktionen sind aber
eben in entgegengesetzter Richtung aufgetragen.
Es ist eben eine Methode, nicht mehr und nicht weniger. Eine Definition Negativer Zahlen ist dafür nicht notwendig.
Als nächstes eine leicht veränderte lineare Funktion.
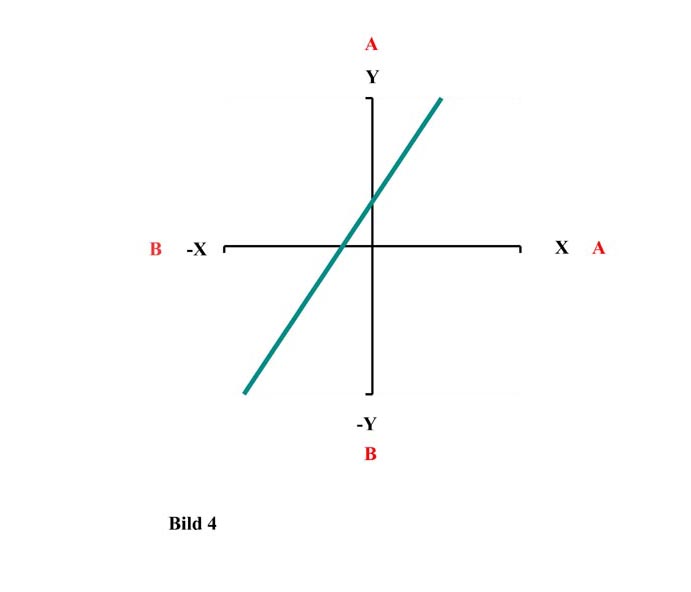
y = k . x + d
k . x + d = 0
k . x = -d
x = - d / k
Auch wieder aus der B-Richtung betrachtet:
y = k . x - d
k . x - d = 0
k . x = d
x = d / k
Ähnliche Funktion, ähnliches Ergebnis.
Die Funktion aus Sicht beider Richtungen aufgelöst führt zum
selben Ergebnis.
Setzt man Zahlen ein und einer der Werte ist Negativ so ändert
sich eben das Vorzeichen wenn man die Zahl einsetzt. Das Negative
Vorzeichen wirkt faktisch als Negationszeichen.
Das ist eine Vereinbarung, auch dazu braucht es keine Definition Negativer Zahlen.
Einfache kubische Gleichung
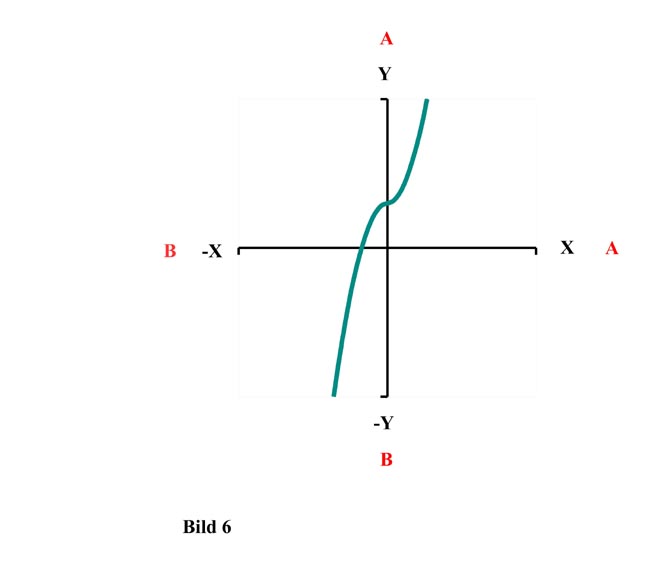
Nun eine einfache kubische Gleichung:

y = x³ + d
x³ + d = 0
x³ = -d
x = ³V(-d)
Aus der B-Richtung betrachtet:
y = x³ - d
x³ - d = 0
x³ = d
x = ³V(d)
Es ist immer das gleiche Prinzip. Der Wert d wirkt aus der A-Richtung betrachtet zwangsläufig
entgegengerichtet und es ergibt sich die entsprechende Funktion daraus, ob es nun die
Division durch k ist oder die 3. Wurzel aus diesem entgegengesetzten Wert.
Einfache Quadratische Gleichung
Nun, natürlich spricht nichts dagegen eine quadratische Gleichung
in der üblichen Form zu definieren, nämlich dass man beim
Quadrat
von (x) eine zweites Minus-Zeichen als ein Negationszeichen betrachtet
und auf diese Weise (x²) in beide Richtungen über der
X-Achse aufgetragen wird. Diese Vorgangsweise ist aber eine Methode, es
gibt aber keinen Grund diese
Methode exklusiv anzuwenden.
Es gibt keinen Grund warum man eine Quadratische Funktion nicht auch in
der Weise definieren kann dass das Quadrat der Negativen Seite
eben auch in die Negative Richtung wirkt.
Das ist die gleiche Vorgangsweise wie sie bei gerichteten
Größen ohnehin oft genug angewandt wird indem man die Regeln
für Negative Zahlen für ungültig erklärt bzw. diese
Regeln ganz einfach ignoriert.
Man muss es nur eindeutig kennzeichnen dass man diese Regel für Negative Zahlen nicht anwenden will.
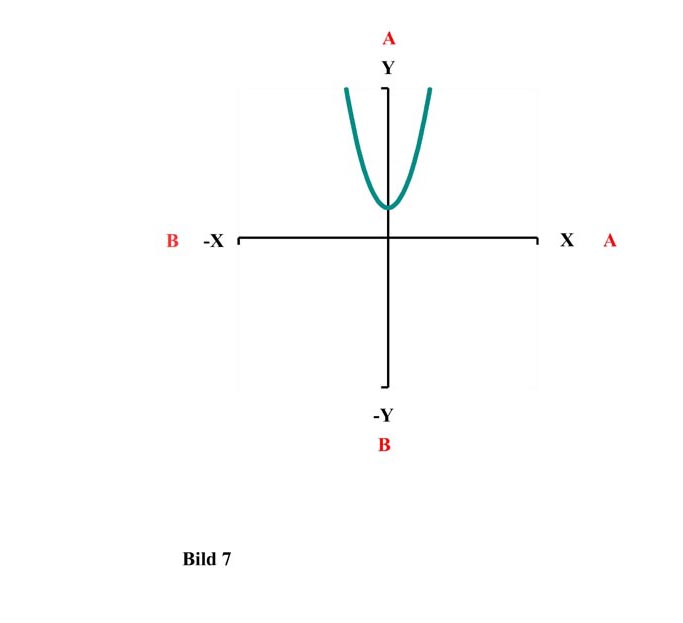
Eine solche Quadratische Funktion sieht dann folgendermaßen aus:
y = x² + d
x² + d = 0
x² = -d
x = ²V(-d)
Aus der B-Richtung betrachtet:
y = x² - d
x² - d = 0
x² = d
x = ²V(d)
Aus der A-Richtung betrachtet ergibt sich eben wieder (-d) und daraus
die Quadratwurzel. Es heißt ganz einfach dass (d)
in
B-Richtung wirkt und daraus dann eben die Wurzel. Daran ist nichts
falsch und es gibt auch keinen Grund warum man diese Wurzel nicht
ziehen sollte.
Man kann die Regeln für Negative Zahlen verwenden, aber man muss es nicht zwangsläufig tun.
Nachdem mit den Negativen Zahlen generell definiert wird dass das
Quadrat eines Negativen Wertes Positiv ist, ist es notwendig diese Wurzel aus
einer Negativen Zahl in irgend einer Weise zu kennzeichnen. Etwa indem man vereinbart diese Zahl in eine Klammer zu schreiben und
dass das Quadrat dieser Zahl auch wieder negativ ist.
Für d = 4 ergibt sich für x:
x = ²V(-d) = ²V(-4) = (-2)
und in den Ansatz für y = 0 eingesetzt:
x² + d = 0
(-2)² + 4 = 0
-4 + 4 = 0
Auf diese Weise schließt sich der Kreis und es ist auch nichts verkehrt an einer solchen Vorgangsweise.
Man kann es natürlich auch in einer etwas anderen Schreibweise
schreiben und das Ergebnis mit einer Kennzahl wie "i" kennzeichnen:
Wenn man dann die Multiplikation so
definiert dass das Quadrat dieser Vorzeichen-Merkzahl wieder eine negative Zahl ergibt
(r1, i1).(r2, i2) = (r1.r2 - i1.i2, r1.i2 + i1.r2), also
(0, 2i) . (0, 2i) = (-4, 0i) = -4
so
erhält man wieder für
x² = -4
Für d = 4 ergibt sich für x:
x = ²V(-d) = ²V(-4) = 2i
und in den Ansatz für y = 0 eingesetzt:
x² + d = 0
(0, 2i) . (0, 2i) + 4 = 0
(-4, 0i) + 4 = 0
-4 + 4 = 0
Das heißt, man
nimmt das Ergebnis aus der Wurzel nicht unmittelbar zur Kenntnis, die
Information bleibt aber erhalten und man kann das Ergebnis in gleicher
Weise in die Ausgangsgleichung einsetzen. Das ist in diesem Fall zwar
nicht notwendig, aber es ist prinzipiell auch nicht falsch. An
diesem einfachen Beispiel sieht man die Funktion dieser Merkregel, also
den so bezeichneten Komplexen Zahlen, sogar besonders gut.
Daran ist aber nichts Komplex und auch
nichts Imaginär, es it ganz einfach eine Vorzeichen-Merkregel, wo
man sich das Negative Vorzeichen mit einem Buchstaben merkt, und
die Multiplikation so defniert ist dass bei der Multiplikation das
Negative Vorzeichen wieder erscheint.
Dass diese Vorzeichen-Merkregel aus einem anderen Grund definiert
wurde, als eine vermeintliche Lösung einer kubischen
Gleichung, ändert daran auch nichts.
Ob negative Ergebnisse überhaupt Sinn machen hängt
natürlich davon ab in welcher Form die Funktion der Gegenrichtung
definiert ist. Dagegen sind positive Werte beider Seiten immer
richtig.
Am sinnvollsten ist es daher
auf beiden Seiten nur positive Lösungen zu verwenden und negative
Ergebnisse überhaupt zu ignorieren.
Man kann dann das Ergebnis beider Seiten immer noch zu einer
Lösungsformel zusammen fügen, wie das bei der Quadratischen
Gleichung in der bekannten Form der Fall ist.
Einfache Quadratische Gleichung ohne Lösung
Hier, nun eine einfache quadratische Funktion in der üblichen Form:
y = x² + d
x² + d = 0
x² = -d
x = ²V-d
Aus der B-Richtung betrachtet:
y = -x² - d
-x² - d = 0
-x² = d
x² = -d
x = ²V-d
Zunächst einmal kann bei der bestehenden Definition mit "Negativen
Zahlen" x² nur positiv sein. Unter der Voraussetzung dass auch d
positiv ist, ist schon der Ansatz
x² + d = 0
sinnfrei. Denn die Summe zweier positiver
Zahlen kann nicht null sein. In diesen Fall ist der Ansatz genau so sinnfrei wie der Ansatz
4 + 2 = 0
Die
Formel für die Lösung quadratischer Gleichungen beinhaltet also, unter
bestimmten Voraussetzungen, einen Ansatz der ein völlig sinnfrei ist.
Sollte
x = 0
sein dann ändert das daran auch nichts denn auch
0 + 2 = 0
ist sinnfrei. Das
allein zeigt dass die Formel für das Lösen quadratischer
Gleichungen nicht generell anwendbar ist und in diesem Fall keinen Sinn
ergibt.
Löst man
x² + d = 0
trotzdem nach x auf so erhält man wieder
x = ²V(-d)
In diesem Fall hat ist der Negative Wert unter der Wurzel
tatsächlich keinen Sinn. Daran ist nichts komplex oder
imaginär, diese Gleichung hat unter diesen Voraussetzungen ganz
einfach keine Lösung.
Einfache Quadratische Gleichung mit Lösung
Eine quadratische Funktion mit Lösung:
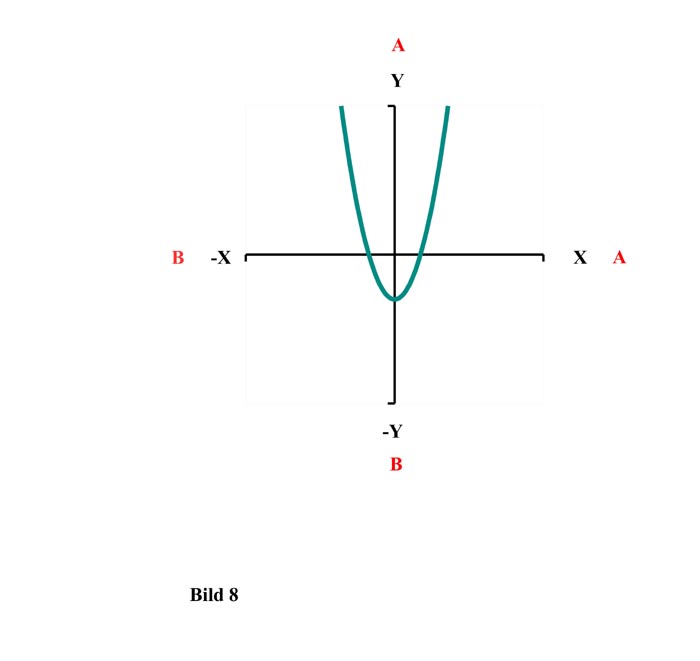
y = x² - d
x² - d = 0
x² = d
x = ²V(d)
Aus der B-Richtung betrachtet:
y = -x² + d
-x² + d = 0
-x² = -d
x² = d
x = ²V(d)
In diesem Fall ergibt sich einfach für beide Seiten A und B eine Lösung.
Hier entspricht das Ergebnis dem Plus/Minus Vorzeichen der
bekannten Lösungsformel für quadratische Gleichungen. Gegen
die
Zusammenfassung zu einer Lösungsformel für diese Form der
Funktion spricht
ja auch nichts, nur dass sie eben nicht unter allen Umständen
anwendbar sein muss.
An dieser einfachen quadratischen Gleichung sieht man es sogar besonders gut.
An sich wird eine quadratische Funktion einmal nach links und einmal
nach
rechts über der X-Achse aufgetragen, was eigentlich zwei Funktionen
sind. Man könnte das in beide Richtungen mit
y = x² - d
anschreiben, einmal nach links, einmal nach rechts bzw. einmal in
A-Richtung und einmal in B-Richtung.
Auch auf diese
Art erhält man für beide Seiten zwangsläufig die gleiche Lösung.
Man kann nun auch die Vereinbarung treffen dass das Vorzeichen der
B-Richtung (Minus Zeichen) gleichzeitig als ein
Negationszeichen verwendet wird, wie es mit der Definition Negativer Zahlen geschieht.
Man kann dann weiter die beiden Funktionen so quasi zu einer
Funktion zusammenfassen und die Lösung beider Seiten mit dem Plus/Minus Zeichen ( + ) angeben. Solange man das als eine solche Vorgangsweise definiert ist daran noch nichts verkehrt.
Nur
wenn man vermeint darin eine
"Existenz" Negativer Zahlen zu erkennen so ist das durch nichts begründet.
Quadratische Gleichungen
Eine weitere Form der quadratischen Gleichung ist:
y = x² - px + q
Hier können sich auf einer Seite
zwei Lösungen ergeben. Auch dies lässt sich
erklären ohne dass man dazu so etwas wie eine Vorstellung
Negativer Zahlen braucht. Zur Veranschaulichung sind rechts die drei
Kurven dargestellt aus denen sich diese Funktion zusammen setzt.
Die beiden Lösungen dieser Gleichung ergeben sich
folgendermaßen.
y = x² - px + q
x² - px + q = 0
x² - px = -q
mit der Formel für das Binom
(a - b)² = a² - 2ab + b²
und
a² = x²
b = p/2 bzw. b² = (p/2)²
ergibt sich:
x² - 2(p/2)x + (p/2)² = (p/2)² - q
(x - p/2)² = (p/2)² - q
x - p/2 = ²V[(p/2)² - q]
x = p/2 + ²V[(p/2)² - q]
Beim Quadrat des Binoms
a² - 2ab + b²
kann sowohl (a) als auch (b) der größere Wert sein .
(a - b)² = a² - 2ab + b²
(b - a)² = a² - 2ab + b²
Das heißt in der Anwendung zur Lösung der Quadratischen Gleichung kann sowohl
a² = x² als auch
b² = (p/2)²
der größere Wert sein. Der zweite Fall führt dementsprechend auch zu einem unterschiedlichen Ergebnis.
x² - 2(p/2)x + (p/2)² = (p/2)²- q
(p/2 - x)² = (p/2)²- q
p/2 - x = ²V[(p/2)²- q]
-x = -p/2 + ²V[(p/2)²- q]
x = p/2 - ²V[(p/2)²- q]
Das heißt wenn man es elementar betrachtet kommt man auch zu zwei
Lösungen, man braucht dazu keine Regeln für Negative Zahlen,
es ergibt sich ganz einfach aus der Regel für die Multiplikation
von Differenzen.
Das (p/2) ist hier deshalb positiv weil ja das Negative Vorzeichen bereits in der Ausgangsgleichung berücksichtigt wurde.
Das (p/2)² unter der Wurzel
ist deshalb immer Positiv weil es ja dem (b²) des Binoms
entspricht und das ist eben immer Positiv. Auch dazu braucht es keine
Vorstellung von Negativen Zahlen.
Wenn der Wert unter Wurzel Negativ ist hat die Gleichung keine Lösung.
In diesem Fall ist aber bereits die Gleichung
x² - px + q = 0
nicht richtig denn dann kann die rechte Seite überhaupt nicht null sein.
Und dann ist auch
x² - px = -q bzw,
x² - 2(p/2)x + (p/2)² = (p/2)²- q
ganz einfach nicht richtig, die beiden Seiten der Gleichung sind dann eben nicht gleich.
Dass der rechte negative Wert später unter der Wurzel steht ist nicht die
Ursache dafür dass die Lösung keinen Sinn ergibt. Unter dieser Voraussetzung ist vielmehr
der Ansatz von Anfang an sinnfrei.
Wenn (px) Positiv ist also
x² + px + q = 0
so erhält man auf der Negativen Seite zwei Lösungen.
Nun, diesen Fall kann man es einfach als
x² - px + q = 0
über der X-Achse nach Links aufgetragen betrachten.
Wenn man das Ergebnis
x = p/2 +
²V[(p/2)² + q]
von der rechten Seite aus betrachtet erhält man
x = -p/2 +
²V[(p/2)² - q]
Auch dafür braucht es
keine Negativen Zahlen, man muß nur das Ergebnis, das sich
auf der linken Seite ergibt, von der rechten Seite aus betrachten.
Wenn (q) Negativ ist
x² - px - q = 0
so erhält man auf der Positiven Seite
x = p/2 + ²V[(p/2)² + q]
Von der Negativen Seite aus betrachtet entspricht dies
x² + px - q = 0
und man erhält
x = -p/2 + ²V[(p/2)² + q]
Von der Positiven Seite aus betrachtet entspricht dies
x = p/2 - ²V[(p/2)² + q]
was einer der beiden Lösung entspricht die man auf der Positiven Seite erhält.
Auch dafür braucht es keine Vorstellungen von Negativen Zahlen.
Natürlich spricht nichts dagegen alle diese Lösungen
zu einer Lösungsformel für quadratische Gleichungen zusammenzufassen
x = -p/2 +
²V[(p/2)²- q]
es ist aber ein Unterschied
ob man darin eine Lösungsformel für quadratische Gleichungen
sieht oder ob man meint hierin so etwas wie eine Existenz Negativer Zahlen sehen zu müssen.
Wenn man darin eine Lösungsformel sieht ist daran durchaus nichts
falsch. Wenn man dagegen darin das Verhalten Negativer Zahlen sehen
will, so ergibt sich schon in der Herleitung
dieser Lösungsformel ein Widerspruch.
(x + p/2)² = (p/2)²- q
x + p/2 = + ²V[(p/2)² - q]
Warum erscheint das Plus/Minus in der zweiten Zeile nur auf der rechten Seite und nicht auf der linken Seite auch?
Denn wenn es nach der Definition Negativer Zahlen geht so müsste das + doch
auf beiden Seiten der Gleichung erscheinen, denn es wird ja auf
beiden Seiten die Wurzel gezogen. Dass auf der linken Seite das Wurzelziehen
einfach durch das Weglassen des Quadrats erfolgt ändert daran gar
nichts. Man stelle sich nur vor dass auf beiden Seiten der
Ausdruck in der ersten Zeile der Zahl 100 entspricht und man diese
Zahlen auch einsetzt, dann hat man in beiden Zeilen folgendes stehen:
100 = 100
10 = + 10
Es ist eben nur die Zusammenfassung der Lösungen einer
quadratischen Gleichung zu einer Lösungsformel. Nicht mehr und
nicht weniger. Denn wenn es wirklich das Verhalten einer Zahlenart
wäre, so müßten diese Regeln für Negative Zahlen
immer gelten. Denn die Regeln für eine Zahlenart gelten eben, oder
sie gelten eben nicht.
Wenn man es einfach als eine Lösungsformel für quadratische Gleichungen ansieht dann besteht kein Widerspruch.
Schlussfolgerung
Die Lösungen für quadratische Gleichungen lassen sich zu
einer Lösungsformel zusammenfassen was später zu einer
Vorstellung von einer Existenz Negativer Zahlen geführt hat. Wenn
man es aber elementar betrachtet, nämlich dass eigentlich zwei
Funktionen in die beiden Richtungen aufgetragen werden, so kann man die
Lösungen auch elementar erklären, es braucht dazu keine
Vorstellung von einer Existenz Negativer Zahlen. Die Definition
Negativer Zahlen in der bestehenden Form ist unbegründet.
Unter dieser Voraussetzung werden im folgenden die Kubischen Gleichungen betrachtet.
Weiter zu
Kubische Gleichungen
Satz_von Vieta
Komplexe Zahlen
Zurück zu
Negative Zahlen
Zurück
zum Anfang
Robert
Markweger
rmw@markweger.at
12. 5. 2025
Copyright © 2025 markweger.at (Eigentümer von markweger.at)







