Robert Markweger
Kubische Gleichungen
Negative Zahlen sind eine
Zusammenfassung von Rechenregeln und
Rechenmethoden. Weiters ist die Negative Seite einer Funktion ganz
einfach eine Funktion die in die Gegenrichtung aufgetragen ist. Unter
dieser Voraussetzung wird hier die kubische Gleichung betrachtet.
Als Quelle für die Ableitung der Kubischen Gleichung werden die folgenden beiden Seiten verwendet:
Gleichung 3 Grades und Cardanische Formel
Wenn man eine kubische Gleichung in der Form
y = x³ + ex² + fx + g
betrachtet und y = 0 setzt:
x³ + ex² + fx + g = 0
und dies mit der 3. Potenz von (a + b) vergleicht
(a + b)³ = a³ + 3a²b + 3ab² + b³
so sieht man gleich dass die Lösung hier nicht so einfach ist
wie bei der quadratischen Gleichung, nachdem hier
das (b) in (3a²b) und (3ab²) für (e) und (f)
in einem quadratischen Verhältnis, also in einem ganz bestimmten
Verhältnis zueinander, vorhanden ist.
Die 3. Potenz von
(a + b + c) führt zum Ausdruck
(a + b +c)³ = a³ + a² . 3(b + c) + a . 3(b + c)² + (b + c)³
Auch hier sind die beiden Ausdrücke für (e) und (f) in einem ganz bestimmten Verhältnis zueinander.
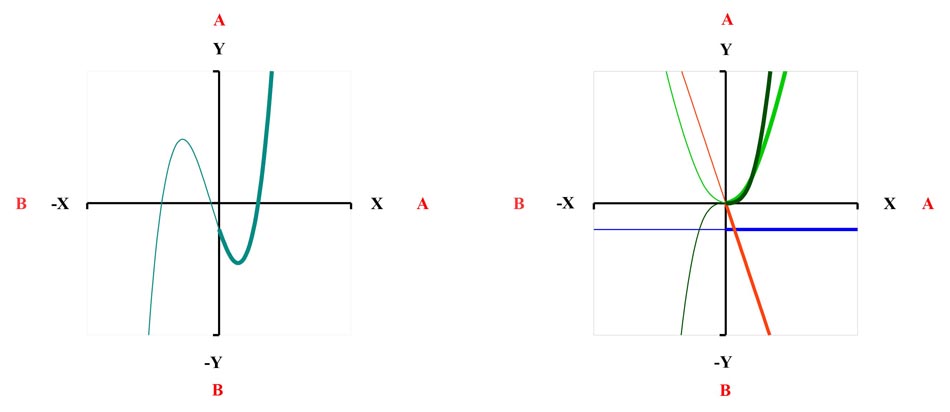
Bild 10
Reduzierte Kubische Gleichung
Die kubische Gleichung
x³ + ex² + fx - g = 0
wird zunächst durch Substitution in eine reduzierte kubische Gleichung umgeändert.
(- g)
wird verwendet damit sich auf der Positiven Seite eine Lösung ergibt.
Substitution
Durch die Substitution von
x = z - e/3
und mit den Formeln für das Binom
(a - b)² = a² - 2ab + b²
(a - b)³ = a³ - 3a²b + 3ab² - b³
fällt das quadratische Element heraus und man erhält damit eine reduzierte kubische Gleichung.
x³ + ex² + fx - g = 0
(z-e/3)³ + e(z-e/3)² + f(z-e/3) - g = 0
z³ - 3z²e/3 + 3ze²/9
- e³/27 + ez² - e2ze/3 + ee²/9
+ fz - fe/3 - g = 0
z³ - z²e + ze²/3 - e³/27 + z²e - 2ze²/3 + e³/9 + fz - fe/3 - g = 0
z³ + z(e²/3 - 2e²/3 + f) - e³/27 + e³/9 - fe/3 - g = 0
z³ + z(f - e²/3) + 2e³/27 - fe/3 - g = 0
Mit
h = (f - e²/3) und
m = 2e³/27 - fe/3 - g
ergibt sich eine reduzierte kubische Gleichung in der Form:
z³ + hz + m = 0
Um auf der Positiven Seite eine Lösung zu erhalten muss
zumindest ein Vorzeichen Negativ sein, was sich aber auf die
Substitution des quadratischen Elements nicht auswirkt.
Für den Fall dass (ex²) negativ ist ergibt sich:
x³ - ex² + fx + g = 0
x = z + e/3
x³ - ex² + fx + g = 0
(z+e/3)³ - e(z+e/3)² + f(z+e/3) + g = 0
z³ + 3z²e/3 + 3ze²/9
+ e³/27 - ez² - e2ze/3 - ee²/9
+ fz + fe/3 + g = 0
z³ + z²e + ze²/3 + e³/27 - z²e - 2ze²/3 - e³/9 + fz + fe/3 + g = 0
z³ + z(e²/3 - 2e²/3 + f) + e³/27 - e³/9 + fe/3 + g = 0
z³ + z(f - e²/3) + 2e³/27 + fe/3 + g = 0
h = (f - e²/3)
m = 2e³/27 + fe/3 + g
Das quadratische Element fällt also auch hier heraus.
Negative Seite:
Wenn man die Negative Seite der Gleichung
x³ + ex² + fx - g = 0
behandeln will, so kann man für die Negative Seite schreiben:
x³ - ex² + fx + g = 0
Dies entspricht der Ableitung für ein Negatives (ex²) der Positiven Seite.
Bzw. bei der Gleichung
x³ - ex² + fx + g = 0
kann man für die Negative Seite schreiben:
x³ + ex² + fx - g = 0
Auf diese Art kann man sicher stellen auch die Negative Seite eindeutig und richtig zu behandeln.
Es gibt schließlich keinen zwangsläufigen Grund dass
die Regeln für Negative Zahlen beliebig funktionieren müssen.
Cardanische Formel
Eine Gleichung mit nur positiven Vorzeichen
z³ + hz + m = 0
kann allerdings auf der positiven Seite keine Lösung haben.
Man kann daher die folgenden Fälle betrachten:
Fall 1:
hz ist Negativ
z³ - hz + m = 0
Auf diese Weise entspricht das Vorzeichen in der folgenden Ableitung immer dem tatsächlichen Vorzeichen. Man sieht daher ob das nachherige Einsetzen
negativer Werte hier auch tatsächlich funktioniert.
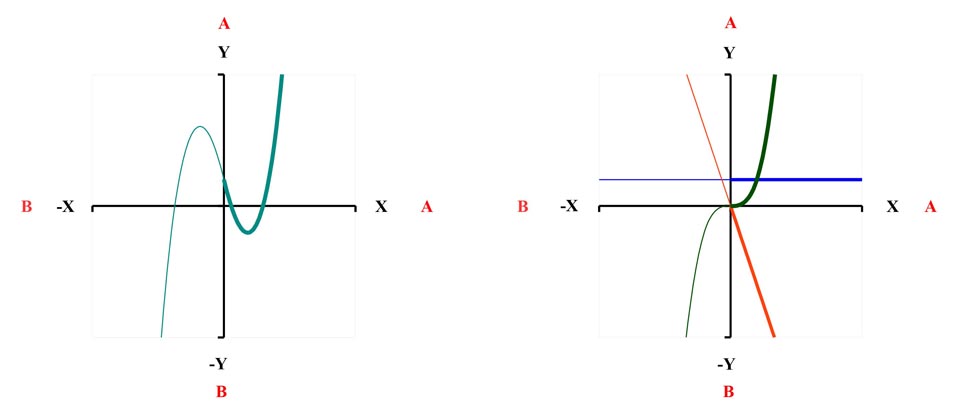
Bild 11
z³ - hz + m = 0
z³ = hz - m
Einsetzen von (u + v) für (z)
z = u + v
(u + v)³ = hz - m
u³ + v³ + 3u²v + 3uv² = hz - m
u³ + v³ + 3uv(u + v) = hz - m
u³ + v³ + 3uvz = hz - m
u³ + v³ + m = hz - 3uvz
Unter der Voraussetzung dass beide Seiten der Gleichung null sind, erhält man zwei Gleichungen.
u³ + v³ + m = 0 = hz - 3uvz
Auf der rechten Seite fällt (z) heraus und man erhält:
hz - 3uvz = 0
h - 3uv = 0/z
h - 3uv = 0
Als zweite Gleichung ergibt sich aus der linken Seite:
u³ + v³ + m = 0
Unter der Voraussetzung dass (z) Positiv ist (z = u + v)
muss also zumindest die Summe aus (u + v) und daher auch (u³ +
v³) positiv sein. Da auch (m) positiv ist, ist daher
u³ + v³ + m = 0
überhaupt nicht möglich. Die Vorzeichen entsprechen hier schließlich den tatsächlichen Vorzeichen.
Die Summe zweier positiver Zahlen (u³ + v³) und (m) kann nicht null sein.
Die weitere Ableitung der Cardanischen Formel ist also für die Vorzeichen
z³ - hz + m = 0
sinnlos.
Setzt man gleich zu Beginn
z = u - v
so erhält man
u³ - v³ + m = 0
was also an der Aussage nichts ändert. Außerdem erhält man
h + 3uv = 0
was ebenfalls nicht null sein kann.
Die Cardanische Formel kann also in diesem Fall von vorn herein zu keinen sinnvollen Ergebnis führen.
Man hat in diesem Fall allerdings über den Umweg einer geometrischen Analogie eine Lösung gefunden.
Negative Seite
Die Negative Seite dieser Gleichung kann man als
z³ - hz - m = 0
nach links aufgetragen betrachten.
Das ist auch gleich der nächste Fall.
Fall 2:
hz und m sind Negativ
z³ - hz - m = 0
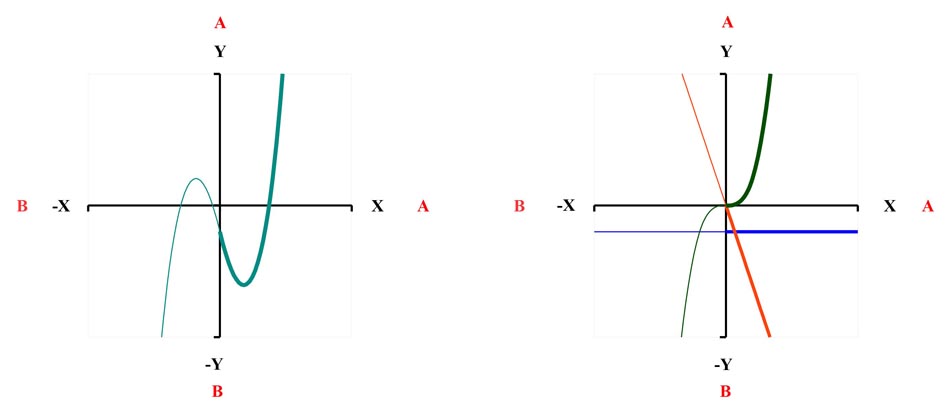
Bild 12
z³ - hz - m = 0
z³ = hz + m
Einsetzen von (u + v) für (z)
z = u + v
(u + v)³ = hz + m
u³ + v³ + 3u²v + 3uv² = hz + m
u³ + v³ + 3uv(u + v) = hz + m
u³ + v³ + 3uvz = hz + m
u³ + v³ - m = hz - 3uvz
Unter der Voraussetzung dass beide Seiten der Gleichung null sind
u³ + v³ - m = 0 = hz - 3uvz
ergibt sich
hz - 3uvz = 0
h - 3uv = 0/z
h - 3uv = 0
und
u³ + v³ - m = 0
Man hat dann die beiden Gleichungen:
u³ + v³ = m
h = 3uv
An den Vorzeichen ist hier nicht zu erkennen dass etwas verkehrt
wäre, was freilich noch nicht ein Nachweis dafür ist dass diese
Nullsetzung auch tatsächlich berechtigt ist.
Es wird aber auch gleich ganz interessant wenn man Zahlen einsetzt:
Mit
u = 2 und v = 2
ergibt sich:
u³ + v³ = m
8 + 8 = 16 n = 16
3uv = h
3 . 2 . 2 = 12 h = 12
Mit
u = 2,5 v = 0,721
ergibt sich:
u³ + v³ = m
15,625 + 0,375 = 16 n = 16
3uv = h
3 . 2,5 . 0,721 = 5,4 h = 5,4
Wenn man v = 0 setzt wird auch h = 0
Das heißt also wenn
u = v
ist, so ergibt sich das größtmögliche (h), bei einem ganz
bestimmten (m).
Bei einem größeren (h) ist auch hier der Ansatz
der Cardanischen Formel sinnlos.
Oder umgekehrt bei einem bestimmten (h) ist der Ansatz bei einem kleineren (m) sinnfrei.
Der Grenzwert ist also mit
u = v
m = u³ + v³
m = 2u³
u = ³V(m/2)
h = 3uv
h = 3u²
u = ²V(h/3)
Grenzwert für h bei einem bestimmten n:
h = 3[³V(m/2)]²
bzw. Grenzwert für m bei einem bestimmten h:
m = 2[²V(h/3)]³
bzw.
m = 2[³V(h/3)]²
m/2 = [³V(h/3)]²
²V(m/2) = ³V(h/3)
²V(m/2) - ³V(h/3) = 0
Das entspricht dem Ausdruck unter der Wurzel der Cardanischen Formel.
Der Ansatz der Cardanischen Formel ist mit den Vorzeichen
z³ - hz - m = 0
also nur bis zu einem bestimmten Verhältnis von (h) und (m) anwendbar!
Wenn dieser Grenzwert überschritten wird ist also auch hier der Ansatz zur Cardanischen Formel sinnlos.
Auch hier hat man über den Ansatz mit einer geometrischen Analogie eine Lösung gefunden.
Setzt man gleich zu Beginn
z = u - v
so erhält man auch hier wieder
h + 3uv = 0
was aber nicht null sein kann.
Im oft zitierten Fall
z³ - 15z - 4 = 0
ergibt sich mit (m = 4) der maximale Wert für (h):
h = 3[³V(4/2)]²
h = 4,76
Da hier aber (h = 15) ist, kann es sich hier beim Ergebnis
(z = 4) nur um einen Zufallstreffer handeln. Dass für ganz
bestimmte Variable eine sinnfreie Vorgangsweise zu einem richtigen
Ergebnis führt ist ja nicht von vornherein ausgeschlossen. Der
Umstand dass
h = 15 und m = 4
die einzigen bekannten
Parameter außerhalb des Anwendungsbereichs sind, die zum richtigen Ergebnis führen, weist auch in
diese Richtung.
Unter der Voraussetzung dass (h) ein bestimmtes Verhältnis zu (m) nicht überschreitet
kann man also mit dem bestehenden beiden Gleichungen fortfahren.
u³ + v³ = m
h = 3uv
h/3 = uv
h³/27 = u³v³
Damit wird der Satz von Vieta anwendbar.
x² - x(x1 + x2) + x1.x2 = 0
mit
x1 = u³
x2 = v³
x² - x(u³ + v³) + u³v³ = 0
bzw.
x² - xm + h³/27 = 0
Mit der Lösungsformel für diese quadratische Gleichung
x = -p/2 + ²V[(p/2)²-q]
wird daher:
x1,x2 = u³,v³ = m/2 + ²V(m²/4 - h³/27)
und mit
z = u + v
z = ³V[m/2 + ²V(m²/4 - h³/27)] + ³V[m/2 - ²V(m²/4 - h³/27)]
bzw. das (x) der nicht reduzierten Gleichung wird mit:
x = z - e/3
x = ³V[m/2 + ²V(m²/4 - h³/27)] + ³V[m/2 - ²V(m²/4 - h³/27)] - e/3
Negative Seite
Die Negative Seite dieser Gleichung kann man mit dem voherigen Ansatz
z³ - hz + m = 0
betrachten.
Fall 3:
Nun noch der einfachere Fall dass nur (m) negativ ist
z³ + hz - m = 0

Bild 13
z³ + hz - m = 0
z³ = - hz + m
Einsetzen von (u + v) für (z)
z = u + v
(u + v)³ = - hz + m
u³ + v³ + 3u²v + 3uv² = - hz + m
u³ + v³ + 3uv(u + v) = - hz + m
u³ + v³ + 3uvz = - hz + m
u³ + v³ - m = - hz - 3uvz
Unter der Voraussetzung dass beide Seiten null sind
u³ + v³ - m = 0 = - hz - 3uvz
erhält man die beiden Gleichungen
u³ + v³ - m = 0
u³ + v³ = m
und
hz + 3uvz = 0
h + 3uv = 0/z
h + 3uv = 0
Der Ausdruck
h + 3uv = 0
kann allerdings nicht null sein, es sei denn (u) oder (v) sind negativ.
Man kann es daher mit dem Ausdruck
z = u - v
versuchen, um auch hier mit tatsächlichen Vorzeichen sicher zu stellen dass es auch tatsächlich funktioniert.
(u - v)³ = - hz + m
u³ - v³ - 3u²v + 3uv² = - hz + m
u³ - v³ - 3uv(u - v) = - hz + m
u³ - v³ - 3uvz = - hz + m
u³ - v³ - m = 3uvz - hz
Unter der Voraussetzung dass beide Seiten null sind
u³ - v³ - m = 0 = 3uvz - hz
ergibt sich wieder
3uvz - hz = 0
3uv - h = 0/z
3uv - h = 0
3uv = h
und
u³ - v³ - m = 0
u³ - v³ = m
An den Vorzeichen dieser beiden Gleichungen ist nun kein Fehler zu
erkennen, was auch hier freilich noch nicht ein Nachweis dafür ist
dass die Nullsetzung tatsächlich berechtigt ist.
Man hat nun also die beiden Gleichungen:
u³ - v³ = m
uv = h/3 bzw.
u³.v³ = h³/27
Damit wird auch hier der Satz von Vieta anwendbar.
x² - x(x1 - x2) - x1.x2 = 0
mit
x1 = u³
x2 = v³
wird
x² - x(u³ - v³) - u³v³ = 0
bzw.
x² - xm - h³/27 = 0
Mit der Lösungsformel für diese quadratische Gleichung
x = -p/2 + ²V[(p/2)² - q]
wird daher:
x1,x2 = u³,v³ = m/2 + ²V(m²/4 + h³/27)
und mit
z = u - v
z = ³V[m/2 + ²V(m²/4 + h³/27)] - ³V[m/2 - ²V(m²/4 + h³/27)]
bzw. das (x) der nicht reduzierten Gleichung wird mit:
x = z - e/3
x = ³V[m/2 + ²V(m²/4 + h³/27)] - ³V[m/2 - ²V(m²/4 + h³/27)] - e/3
Weiter zu
Satz von Vieta
Komplexe Zahlen
Zurück zu
Negative Zahlen
Lineare und Quadratische Gleichungen
Zurück
zum Anfang
Hier sind noch einmal die beiden Links zur Ableitung der Kubischen Gleichung:
Gleichung 3 Grades
Cardanische Formel
Robert
Markweger
rmw@markweger.at
12. 5. 2025
Copyright © 2025 markweger.at (Eigentümer von markweger.at)



